Los autómatas cuánticos son, como su contraparte clásica, modelos de computación. La investigación en esta área está un poco dividida. Existen investigadores que sostienen que la conexión de estos modelos con la realidad no es clara y no poseen una realización física, no así los autómatas clásicos, que bien todos conocen claramente sus aplicaciones y su importancia teórica. Aclaro que aquí no incluyo a los autómatas celulares cuánticos. La aplicación de este último está bien estudiada y existe una relación clara con la realidad, como se puede observar haciendo una simple búsqueda por Google. Aquí me estoy refieriendo a los típicos autómatas como autómatas de estado finito, los autómatas de pila o pushdown, etc. Por otro lado, existen investigadores que sostienen que el estudio de estos modelos es importante para entender las ventajas y desventajas de la computación cuántica, y la relación que existe entre el mundo clásico y el cuántico. A mi en particular me interesa desde un punto de vista netamente de la teoría de lenguajes. En esta entrada voy a presentar una propuesta de autómata cuántico para lenguajes omega (i.e., lenguajes con cadenas de longitud infinita), y algunos problemas abiertos.
Primero, definamos formalmente un lenguaje omega (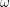
-languages).
Definición 1 (lenguaje-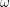 [1]). Sea 
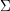un alfabeto y L un lenguaje sobre 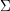. El conjunto de cadenas de longitud infinita sobre 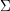es denotado por 
. 
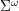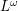es el conjunto de cadenas en 
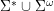que surge de la concatenación de cadenas en 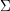. Formalmente, 
.
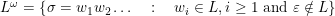Existen dos clases de autómatas clásicos. Primero están los 1-way finite automata (1FA), donde la unidad de control lee un símbolo de entrada y se mueve inmediatamente al siguiente símbolo a la derecha. En segundo lugar están los 2-way finite automata (2FA), donde la unidad de control puede mover el cabezal a la izquierda, derecha, o quedarse en su lugar. Clásicamente, los modelos 1FA y 2FA son equivalentes, pero en el caso cuántico, el poder de reconocimiento de lenguajes cambia radicalmente. Para un tratado completo sobre las diferencias entre el 1FA y 2FA cuánticos referirse a [2].
A continuación presento la definición del autómata cuántico de 1 lado (1-way).
Definición 2 (autómata cuántico de 1 lado [2]). Un autómata cuántico de 1 lado (1QFA) es una tupla )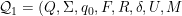
donde - Q es en un conjunto finito de estados,
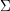- es el alfabeto de entrada, - 
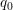es el estado inicial, - F es el conjunto de estados de aceptación o finales,
- R es el conjunto de estados de rechazo con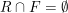 
, - \times%20Q\to\mathbb{C}_{[0,1]})
es la función de transición donde 
y 
son marcadores de inicio y final de cadena, y para un símbol 
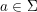y estados q,r, se tiene que |^2\in[0,1])
, - 
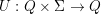o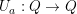 
para algún 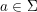es un operador unitario (i.e., 
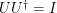) tal que |r\rangle$)
, - 
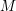es un observable definido en la base de 
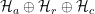, donde 
, 
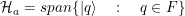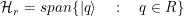, y 
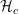es el complemento ortogonal de 
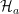y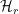 
.
La computación de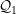 
para una entrada 
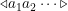es como sigue [2]. El operador 
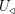se aplica al estado inicial 
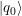y luego 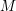es aplicado a 
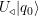. El operador 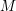proyecta 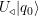a un vector 
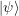en uno de los subespacios 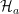, , 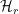, 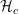con probabilidad igual a 
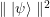. Si 
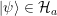la entrada es aceptada y 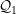para; si 
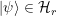la entrada es rechazada y 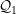para; si 
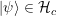entonces se vuelve a aplicar el operador 
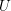a 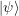para el siguiente símbolo de entrada y el proceso continua. La computación solo continua si ocurre una proyección en .
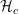Teniendo en cuenta la definición de un autómata cuántico, es fácil extender el autómata para operar con lenguajes-.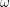
Definición 3 (autómata cuántico 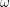de 1 lado). Un autómata cuántico 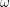de 1 lado es una tupla )
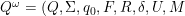donde - Q es en un conjunto finito de estados,
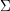- es el alfabeto de entrada, - 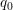es el estado inicial, - F es el conjunto de estados de aceptación o finales,
- R es el conjunto de estados de rechazo con 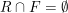, - \times%20Q\to\mathbb{C}_{[0,1]})
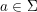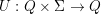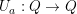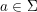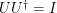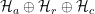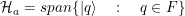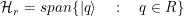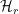es la función de transición donde es el marcador de inicio de cadena, y para un símbol y estados q,r, se tiene que , - o para algún es un operador unitario (i.e., ) tal que , - M es un observable definido en la base de , donde , , y es el complemento ortogonal de 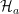y .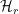
La computación de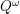 
para una entrada 
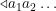es de la misma forma que el QFA 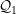. La diferencia está en que 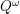lee una cadena de longitud infinita, y por lo tanto la condición de aceptación cambia. De acuerdo a la condición de aceptación de Büchi [3], en una corrida de aceptación el autómata visita los estados 
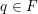infinitamente, porque la cadena de entrada es de longitud infinita. Para el caso cuántico, el resultado de la observación genera una secuencia infinita de estados 
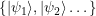. Si el resultado de la observación es un estado de 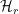o la entrada es finita, 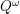rechaza y para. En cambio, si existe un número infinito de vectores en la secuencia con una proyección no vacía en el subespacio 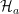se acepta la entrada.
Problemas Abiertos
- Definición de probabilidad de aceptación de lenguajes. Para autómatas 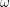clásicos, el autómata se reduce a una cadena de Markov, y la probabilidad de aceptación de una corrida puede definirse en esos términos [3]. Tal vez lo mismo pueda hacerse para 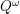, pero usando en su lugar Quantum Walks [4].
- Brecha en la complejidad espacial. En el artículo de Ambainis y Nahimovs [5], se demuestra una brecha exponencial en la complejidad espacial entre el 1FA y el 1QFA para un lenguaje regular específico. Existe un lenguaje- 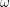con una brecha exponencial en complejidad espacial?.
- Reconocimiento de lenguajes. Si un 1QFA acepta un lenguaje L, entonces L es regular [2]. Pero, se sabe que la clase de lenguajes de los 1QFA está estrictamente incluido en la clase de lenguajes de los FA [2]. Cuáles son las propiedades de reconocimiento de lenguajes de los autómatas cuánticos ?.
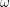Referencias
[1] Christel Baier y Joost-Pieter Katoen. Principles of Model Checking. MIT Press, 2008.
[2] Josef Gruska. Quantum Computing. McGraw Hill, 2000.
[3] Christel Baier, Nathalie Bertrand, y Marcus Größer. The Effect of Tossing Coins in Omega-automata. In: Proceedings of CONCUR'09, pages 15-29, 2009.
[4] Julia Kempe. Quantum Random Walks - An Introductory Overview. arXiv:quant-ph/0303081.
[5] Andris Ambainis y Nikolajs Nahimovs. Improved Constructions of Quantum Automata. Theoretical Computer Science, 410(20):1916-1922, 2009.
