La importancia de P vs NP

Figura de Theory Matters Wiki.

Dado los acontecimientos de la semana que acaba de terminar, donde Vinay Deolalikar presentó un intento de prueba para el problema de P vs NP, esta entrada la escribo para poder explicar los alcances del problema mismo para las ciencias de la computación, y para todas las ciencias en general.

Cada mes se publican en ArXiv artículos que dicen resolver el problema. Algunos dicen que P=NP, otros que P≠NP, etc. La diferencia estuvo en que este artículo en particular había pasado todos los exámenes que utilizan los teóricos en complejidad para discriminar los artículos serios. Además, este estaba escrito por una persona conocida, y cuando  había enviado una versión preliminar a un grupo selecto de científicos, uno de los principales, el mismo descubridor del problema y ganador del premio Turing, Stephen Cook, había escrito en respuesta "esto parece un esfuerzo serio" (del inglés this looks like a serious effort). Esto había motivado al resto y puso a funcionar una máquina bien aceitada de colaboración científica inigualable en la red. Como lo dijo Dick Lipton, "lo que antes se hacía en meses, ahora por Internet lo hacemos en días". Para saber como terminó toda la historia recomiendo el post anterior de Alejandro donde tienen todos los enlaces. Aquí me voy a concentrar en la definición e importancia de P vs NP.

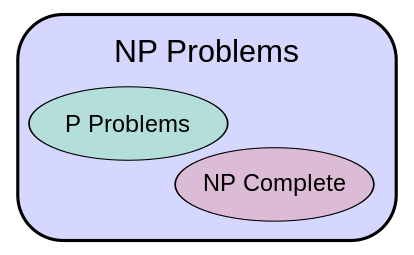
A continuación un pequeño repaso del problema. Antes que nada este es considerado el problema principal, más importante, de las ciencias de la computación. Básicamente el problema es "para ciertos problemas, lo mejor que podemos hacer es una búsqueda bruta", o como escribe Lipton "para ciertos problemas el algoritmo más obvio es el mejor". NP como sabemos quiere decir "tiempo polinomial no-determinístico", y P "tiempo polinomial determinístico". Entonces los problemas o lenguajes con algoritmos que corren en tiempo polinomial están en P, y los problemas con algoritmo en tiempo polinomial no-determinístico en NP.

Una caracterización más fácil de entender de problemas en NP es la siguiente: Sea A un algoritmo que tiene dos entradas, x que representa una instancia de un problema L (e.g. SAT, TSP, etc), y c que representa una solución al problema. Entonces L están en NP si y solo si existe un algoritmo determinístico que corre en tiempo polinomial A y existe un c tal que A(x,c)=1, i.e. que c sea una respuesta válida al problema. Generalmente a c se le llama solución, certificado, testigo o simplemente prueba, i.e. una prueba de que x tiene solución. La misma caracterización se puede hacer para P, pero esta vez el algoritmo no tiene una prueba c. Entonces decimos que L está en P si y solo si existe un algoritmo determinístico que corre en tiempo polinomial A  tal que A(x)=1.

La gran diferencia está en el certificado. Los algoritmos para lenguajes en P determinan una solución, mientras que los algoritmos para lenguajes en NP verifican una solución. Una buena analogía es: si yo resuelvo un problema matemático por mi mismo (está en P), o estoy verificando la solución de otra persona (en NP). Entonces, la diferencia radica en que estamos comparando un proceso de determinar una solución a un problema contra un proceso de verificación de una solución ya dada para un problema.

Imagen de Wikipedia.

P vs NP en términos computacionales se refiere a cotas inferiores de problemas NP-completos. La conjetura es que para estos problemas no existe un mejor algoritmo que el de fuerza bruta, i.e. P≠NP. La mayoría de los científicos creen que esto es cierto, y de ahí surgen un montón de alternativas para resolver problemas NP-completos como Búsqueda Local, Algoritmos Genéticos, etc. Y la eficiencia de estos métodos está en que pueden verificar soluciones en tiempo polinomial.

En mi humilde opinión, una prueba de que P≠NP no cambiaría mucho las cosas porque todo lo que hacemos ahora, lo hacemos en función de que P≠NP. Por ejemplo, asumimos la existencia de 1-way functions en criptografía ¿Entonces de que nos sirve una prueba de eso? Una prueba no solo nos dice si una hipótesis es falsa o verdadera, sino que al mismo tiempo ganamos mucha información acerca del problema mismo. De una prueba de P≠NP podemos descubrir muchas conexiones entre áreas de conocimiento u objetos que creíamos desconectados en nuestra teoría. Eso tiene mucho más valor que una respuesta de falso o verdadero. Esto es lo que está ocurriendo con la prueba de Deolalikar. Algunas personas nunca habían considerado conectar el finite model theory con el clustering en Random-k-SAT. El enfoque de por sí requiere más investigación y despierta mucha curiosidad.

En el aspecto filosófico, P vs NP hace la siguiente pregunta: ¿Puede la creatividad ser automatizada? Si yo escribo un libro en el que trabaje 1 año, y lo mando a un periódico para que un crítico lo lea, y la destruye completamente en 2 semanas, ¿Qué es más dificil, escribir el libro o criticar el libro? Intuitivamente el proceso creativo es más complejo y requiere más tiempo, pero hasta que no tengamos una prueba que indique sin duda alguna nunca sabremos, por la misma razón que expuse en el párrafo de arriba. Simplemente por la curiosidad del hombre, tenemos que saber (esto lo dijo David Hilbert). 

También la misma pregunta se extiende a otros ámbitos como la física. La visión de las ciencias de la computación y una parte de la comunida de físicos, es que toda nuestra realidad física es computable. Desde la evolución de los seres vivos, hasta la formación de galaxias. Todo es visto como un proceso que dado una entrada genera un salida. Entonces salen preguntas como ¿Qué tan complejo es el plegado de proteínas? ¿Qué pasa con la información y la energía en un hoyo negro que se disipa en forma de radiación de Hawking? etc, etc. Muchas de esta preguntas están siendo respondidas por técnicas de ciencias de la computación. Por ejemplo, sabemos que si P≠NP entonces no podemos viajar en el tiempo, o no podemos movernos más rápido que la luz, y otras conexiones más extrañas. Aún así, estás conexiones dan evidencia a favor de que P≠NP, o no?

Asi que P vs NP no solo se refiere a problemas que solo interesan a las ciencias de la computación. Se refiere también a problemas fundamentales de otras ciencias. Inclusive podría decirse que es una de las preguntas más fundamentales de las matemáticas. Saber si podemos encontrar pruebas eficientemente nos da conocimiento de como resolver otros problemas muy difíciles como la Hipótesis de Riemann. Es por ello que el Clay Mathematics Institute lo pone en su lista de problemas fundamentales.

Para más información recomiendo el libro Computational Complexity A Modern Approach, o el artículo de Lance Fortnow en Communications of the ACM.