Circuito para distinguir estados de Bell desconocidos.

Recorriendo la Base de Datos de Los Alamos me he topado con un paper[1] más que interesante. Se trata de un circuito que logra distinguir entre los 4 estados de Bell, sin medirlos y sin destruirlos. El circuito planteado es el que muestro a continuación:

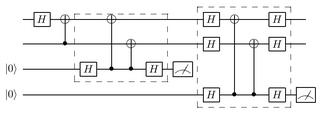
Es un circuito ingenioso que logra dejar en los dos qubits ancillares los valores de los qubits que generan el susodicho estado de Bell.
Me pareció un circuito muy "atractivo" hasta que noté que el mismo resultado puede conseguirse sin mucho esfuerzo "desentangleando" el estado de Bell y volviendo a entanglearlo, de esta manera:

por lo que el circuito anterior pierde todo sentido. En otro paper[2] hablan de cómo utilizar este algoritmo para clonar estados de Bell y el autor termina comparando su método con la Universal Cloning Machine[3] (UCM) diciendo que el suyo es extremadamente mejor ya que puede clonar con fidelidad 1, mientras que la UCM sólo lo hace con una fidelidad de 5/6. En realidad la cuestión es que la UCM clona cualquier estado desconocido, en comparación con éste algoritmo que copia sólo estados de Bell, los cuales pueden ser copiados por más de un método, ya que el Teorema de No-Clonning lo que dice es que no se pueden clonar estados no-ortogonales, y los estados de Bell son ortogonales entre si.

Referencias

[1] M. Gupta, P. K. Panigrahi, "Deterministic Bell State Discrimination", arXiv:quant-ph/0504183 (2005).
[2] J. O. Grabbe, "Deterministic cloning of an unknown Bell state", arXiv:quant-ph/0507016 (2005).
[3] D. Bruss, D. P. DiVincenzo, A. Ekert, C. A. Fuchs, C. Macchiavello, J. A. Smolin, "Optimal Universal and State-Dependent Quantum Cloning", Phys. Rev. A 57 2368 (e-print arXiv:quant-ph/9705038) (1998)