En este post voy a explicar la técnica más popular para la construcción de algoritmos cuánticos conocida como Amplificación de Amplitud (Amplitude Amplification). Mi investigación está principalmente basada en encontrar cotas superiores e inferiores utilizando esta técnica y quantum walks (sobre este punto ya hablaré más adelante). Esta técnica es una generalización del algoritmo de Grover.
Antes que nada, se le llama amplificación de amplitud porque se amplifica o incrementa la amplitud en la ecuación de onda de una partícula. Por ejemplo, sea 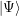 un estado cuántico definido en un espacio de Hilbert
un estado cuántico definido en un espacio de Hilbert  , donde cada
, donde cada 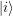 es un vector de la base de
es un vector de la base de 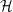 (siempre
(siempre 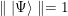 ). En un problema de búsqueda sin información, para encontrar un índice dado
). En un problema de búsqueda sin información, para encontrar un índice dado 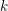 , donde
, donde 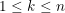 , la técnica de amplificación de amplitud ubica el vector base
, la técnica de amplificación de amplitud ubica el vector base 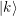 en
en 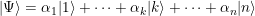 con amplitud
con amplitud 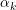 , y sustituye ese valor por otro
, y sustituye ese valor por otro 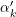 tal que
tal que 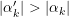 . El resto de las amplitudes son sustituidas por otras amplitudes con valor absoluto menor. Esto ocurre automáticamente porque las transformaciones efectuadas a
. El resto de las amplitudes son sustituidas por otras amplitudes con valor absoluto menor. Esto ocurre automáticamente porque las transformaciones efectuadas a 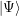 son unitarias, i.e., preservan el valor del producto interno y por lo tanto las normas. De esta forma al realizar una observación, el algoritmo retorna el valor
son unitarias, i.e., preservan el valor del producto interno y por lo tanto las normas. De esta forma al realizar una observación, el algoritmo retorna el valor 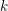 con probabilidad
con probabilidad 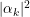 suficientemente alta.
suficientemente alta.
Esa es básicamente la intuición en el algoritmo de amplificación de amplitud. A continuación paso a formalizar esta idea, pero solamente describiendo el caso particular del algoritmo de Grover. Hacia el final de post mencionaré como es el caso general de amplificación sin entrar en detalles.
El algoritmo de Grover funciona aplicando primero al estado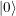 un operador que genera el vector
un operador que genera el vector
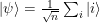 ,i.e., una superposición con la misma amplitud para todos los elementos de la base. Luego, sobre
,i.e., una superposición con la misma amplitud para todos los elementos de la base. Luego, sobre 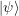 se aplica un número
se aplica un número 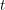 de veces dos operadores unitarios: el oráculo
de veces dos operadores unitarios: el oráculo 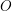 y el operador de difusión
y el operador de difusión 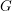 . Entonces el algoritmo luce algo como
. Entonces el algoritmo luce algo como ^t|\psi\rangle) . Vamos a probar que
. Vamos a probar que ) , y retorna
, y retorna 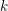 con una probabilidad
con una probabilidad ) .
.
Primero el oráculo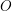 es un operador de fase (reflexión), y su acción se basa en cambiarle el signo a la amplitud de la base
es un operador de fase (reflexión), y su acción se basa en cambiarle el signo a la amplitud de la base 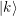 dejando el resto sin alterar. Se define como
dejando el resto sin alterar. Se define como \rangle) , donde
, donde  es la entrada a la función del oráculo, y
es la entrada a la función del oráculo, y 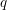 es el bit del oráculo el cual se invierte si
es el bit del oráculo el cual se invierte si =1) (el operador
(el operador 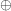 representa al OR exclusivo bit a bit si la codificación es binaria, o puede considerarse como adición modulo 2 para números en base mayor a 2). Inicializando
representa al OR exclusivo bit a bit si la codificación es binaria, o puede considerarse como adición modulo 2 para números en base mayor a 2). Inicializando 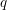 a
a /\sqrt{2}) , la acción del oráculo puede resumirse en
, la acción del oráculo puede resumirse en
^{f(x)}|x\rangle) ,
,
i.e., el oráculo "marca" el vector buscado inviertiendo su fase. Como escribir el oráculo en esta forma dada la definición anterior es un ejercicio muy entretenido (ref. Quantum Information and Computation. Nielsen and Chuang).
El operador de difusión de Grover (definido aquí) tiene la siguiente forma
 ,
,
o en notación de Dirac
 |i\rangle\langle i|+\sum_{i\neq j} \frac{2}{n}|i\rangle\langle j|) .
.
Este operador se conoce también con el nombre de reflexión alrededor de la media, porque también puede escribirse de la siguiente forma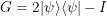 .
.
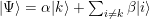 .
.
El algoritmo de Grover funciona aplicando primero al estado
Primero el oráculo
i.e., el oráculo "marca" el vector buscado inviertiendo su fase. Como escribir el oráculo en esta forma dada la definición anterior es un ejercicio muy entretenido (ref. Quantum Information and Computation. Nielsen and Chuang).
El operador de difusión de Grover (definido aquí) tiene la siguiente forma
o en notación de Dirac
Este operador se conoce también con el nombre de reflexión alrededor de la media, porque también puede escribirse de la siguiente forma
Ahora, supongamos que estamos buscando un único elemento 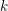 en
en ![[n] [n]](http://latex.codecogs.com/gif.latex?\100dpi%20\inline%20[n]) (esta es una notación más corta para referirse al conjunto
(esta es una notación más corta para referirse al conjunto 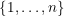 ). Definamos el estado cuántico
). Definamos el estado cuántico
La norma de los vectores debe de ser siempre 1, por lo tanto \beta^2=1) (tenemos un solo
(tenemos un solo 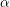 porque solo hay un único vector objetivo, y
porque solo hay un único vector objetivo, y \beta) porque esos vectores no representan una solución al problema). Denotemos por
porque esos vectores no representan una solución al problema). Denotemos por }) el estado del algoritmo en el tiempo
el estado del algoritmo en el tiempo 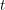 . Vamos a calcular cual es la realción entre
. Vamos a calcular cual es la realción entre }) y
y }) . Primero aplicamos el oráculo
. Primero aplicamos el oráculo
}=-\alpha|k\rangle+\sum_{k\neq i}\beta|i\rangle) .A continuación aplicamos el operador
.A continuación aplicamos el operador 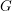 , y obtenemos
, y obtenemos
=\\\begin{array}{ll}&=-\alpha(\frac{2}{n}-1)|k\rangle-\sum_{i\neq k}^n \alpha \frac{2}{n}|i\rangle+\left(\sum_{i=1}^n (\frac{2}{n}-1)|i\rangle\langle i|\right)\left(\sum_{i \neq k}\beta|i\rangle\right)\\&=\alpha\frac{(n-2)}{n}|k\rangle-\alpha\sum_{i\neq k}^n\frac{2}{n}|i\rangle+\sum_{i\neq k}^n(\frac{2}{n}-1)\beta|i\rangle+\beta\frac{2}{n}\sum_{i\neq k}^n(n-2)|i\rangle+\beta\frac{2}{n}(n-1)|k\rangle\end{array}) .
.
El último término requiere un poco de trabajo, pero es simple algebra. Por último, factorizamos los vectores y
![|\Psi\rangle^{(t+1)}=\left[\frac{(n-2)}{n}\alpha+2\frac{(n-1)}{n}\beta\right]|k\rangle+\left[\frac{(n-2)}{n}\beta-\frac{2}{n}\alpha\right]\sum_{i=1}^n|i\rangle |\Psi\rangle^{(t+1)}=\left[\frac{(n-2)}{n}\alpha+2\frac{(n-1)}{n}\beta\right]|k\rangle+\left[\frac{(n-2)}{n}\beta-\frac{2}{n}\alpha\right]\sum_{i=1}^n|i\rangle](http://latex.codecogs.com/gif.latex?\100dpi%20\inline%20|\Psi\rangle^{(t+1)}=\left[\frac{(n-2)}{n}\alpha+2\frac{(n-1)}{n}\beta\right]|k\rangle+\left[\frac{(n-2)}{n}\beta-\frac{2}{n}\alpha\right]\sum_{i=1}^n|i\rangle) .
.
A partir de esta ecuación podemos escribir el estado como
}=\sin((2t+1)\theta)|k\rangle+\sum_i\frac{1}{\sqrt{n-1}}\cos((2j+1)\theta)|i\rangle)
donde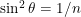 . Esto lo escribo sin demostrar, debido a que la prueba es larga y bastante laboriosa, pero puede obtenerse con simple algebra.
. Esto lo escribo sin demostrar, debido a que la prueba es larga y bastante laboriosa, pero puede obtenerse con simple algebra.
Ahora necesitamos que la amplitud de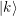 sea cercana a 1, y el resto sea cercano a 0. Si
sea cercana a 1, y el resto sea cercano a 0. Si 4\theta) el coseno se vuelve 0, pero el problema es que ese número no es necesariamente un entero. Entonces elijamos un entero
el coseno se vuelve 0, pero el problema es que ese número no es necesariamente un entero. Entonces elijamos un entero 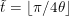 . Tenemos que
. Tenemos que \theta-(2t+1)\theta| \leq \theta) y
y \theta)=\pi/2) implican
implican\theta)\leq\sin\theta) . Por lo tanto, para un ángulo pequeño
. Por lo tanto, para un ángulo pequeño 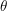 ,
, \theta) \leq \sin^2\theta=1/n) . De esta forma la probabilidad de éxito, i.e., la probabilidad de obtener el vector
. De esta forma la probabilidad de éxito, i.e., la probabilidad de obtener el vector 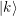 es
es 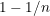 .
.
El algoritmo original de Grover realizaba este procedimiento con 50% de probabilidades de éxito, aquí (utilizando una técnica presentada en este paper) probamos que la probabilidad de éxito está muy cercana a 1 si se elige apropiadamente el número de iteraciones. En este caso) . Si hacemos más iteraciones, debido a la oscilación del estado, la probabilidad de éxito disminuye. Por lo tanto debemos hacer exactamente esa cantidad de iteraciones o un número cercano.
. Si hacemos más iteraciones, debido a la oscilación del estado, la probabilidad de éxito disminuye. Por lo tanto debemos hacer exactamente esa cantidad de iteraciones o un número cercano.
De similar manera podemos demostrar que si tenemos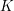 objetos marcados, podemos encontrar uno de esos objetos en
objetos marcados, podemos encontrar uno de esos objetos en ) con
con 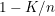 probabilidades de éxito.
probabilidades de éxito.
En el caso general nuestra iteración principal^t|\psi\rangle) la podemos escribir de la siguiente forma
la podemos escribir de la siguiente forma
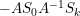
donde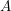 es un operador unitario,
es un operador unitario, 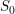 cambia el signo de la amplitud si es el vector 0, y
cambia el signo de la amplitud si es el vector 0, y 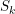 es el oráculo que cambia el signo al vector
es el oráculo que cambia el signo al vector 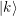 . Para los detalles de las demostraciones para el caso general consultar el paper Quantum Amplitude Amplification and Estimation. Para el caso del algoritmo de Grover tenemos que
. Para los detalles de las demostraciones para el caso general consultar el paper Quantum Amplitude Amplification and Estimation. Para el caso del algoritmo de Grover tenemos que 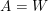 .
.
Otro problema es intentar encontrar todos los objetos marcados, para ello se requiere) con una probabilidad de éxito de
con una probabilidad de éxito de }) .
.
Se puede demostrar también que esta cota superior es óptima, i.e., existe una cota inferior del mismo orden. Pero esa demostración queda para otro día.
El último término requiere un poco de trabajo, pero es simple algebra. Por último, factorizamos los vectores y
A partir de esta ecuación podemos escribir el estado como
donde
Ahora necesitamos que la amplitud de
El algoritmo original de Grover realizaba este procedimiento con 50% de probabilidades de éxito, aquí (utilizando una técnica presentada en este paper) probamos que la probabilidad de éxito está muy cercana a 1 si se elige apropiadamente el número de iteraciones. En este caso
De similar manera podemos demostrar que si tenemos
En el caso general nuestra iteración principal
donde
Otro problema es intentar encontrar todos los objetos marcados, para ello se requiere
Se puede demostrar también que esta cota superior es óptima, i.e., existe una cota inferior del mismo orden. Pero esa demostración queda para otro día.

Bien ahí Marcos! Aunque mis conocimientos técnicos son de otra área,y por lo tanto no entiendo mucho de lo que hablás acá,te felicito por la iniciativa, que será de utilidad para tus colegas. Un saludo!
ResponderBorrar