Estuve probando un poco de MathOverflow y realmente me sorprendió lo rápido en que las personas leen y responden a tus preguntas. La pregunta que hice fue sobre el número de soluciones para sumas de subconjuntos (subset sums). Sea Fq un campo finito con característica p tal que p < q (i.e. no es un campo primo). Sea D ⊆ Fq un subconjunto con |D| = n. El problema de la suma de subconjuntos consiste en encontrar un subconjunto no vacío {x1,…,xk}⊆ D tal que x1 + ... xk = s dado s ∈ Fq. Cuántas soluciones aproximadamente permite el problema para un conjunto dado D? Que pasa si seleccionamos D en forma aleatoria?
La respuesta que obtuve fue la siguiente (la versión escrita aquí está mas desarrollada): Tenemos n elementos de los cuales k tienen que sumar s, entonces tenemos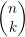 
candidatos. Sea D = {a1,…,an} y definamos la variable aleatoria X como la suma de k elementos de D, i.e. X = ax1 + ... + axk. Las variables xi son índices. Tenemos asi que Pr(X = 0) = P(X = 1) =
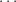= P(X = s) = 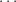P(X = q - 1) = 
. Por lo tanto el número aproximado de soluciones que suman s es claramente 
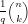. Bien sencillito.
Para el caso D aleatorio supongamos que tenemos una solución x1 + ... + xk. Para una D aleatoria con |D| = n la probabilidad p de que todas las xi en la solución esten presentes en D es
El numerador es así porque para la solución dada solo combinamos los elementos que son diferentes a cada xi. Entonces p es igual para cada solución. Considerando que el número total de soluciones para todo el campo es 
(cf. párrafo de arriba), haciendo cuentas el valor esperado es
Claramente ambas respuestas deben de coincidir porque en el fondo para responder la primera pregunta hacemos uso de índice aleatorios.
Obs: Esta entrada la escribí usando TtH y el Online LaTeX Equation Editor en modo de prueba. La conclusión es utilizar TtH, y lo que no pueda convertir a html, hacerlo con el editor de ecuaciones.
