IHP, allí voy!

Me han aceptado en los cursos que se dictarán en el Instituto Henri Poincaré (que comenté en un post anterior), me asignaron la oficina 322 donde estaremos 3 canadienses, 1 francés, 3 estadounidenses, 1 turco, 1 inglés, 1 japonés, 2 alemanes, 1 maldoví, 2 italianos, 1 austríaco, 1 coreano, 1 taiwanés, 1 indú, 1 holandés, 1 portugués, 1 belga, 1 mexicano, 1 israelí y yo (argentino).

Luego de allí (que estaré sólo el mes de Febrero), Manuel Gadella, de la Universidad de Valladolid, España, me invitó a ir a su universidad un par de semanas a continuar una investigación que estamos haciendo en conjunto.

Aún estoy buscando beca (se aceptan sugerencias), hasta ahora he conseguido medio pasaje por medio del Ministerio de Migraciones (Argentina), mi estadía en España ya está arreglada, lo que aún estoy buscando es abaratar la estadía en París.

PD: A los lectores de este blog, les pido disculpas porque hace un tiempo que no posteaba nada (he estado con demasiadas tareas juntas) y ahora posteo algo más bien de tono personal... ya volveré a postear cosas interesantes ;)

Lista de correo de Computación Cuántica

Les comento, estamos haciendo una lista de correo de discusión general sobre computación cuántica junto con Alan Aspuru-Guzik. Recién hoy la arrancamos, pero la idea es que ahí se puedan hacer preguntas y comentarios sobre el tema.

A todos los que les interese, aquí* tienen la página (luego veremos de agregarle más contenido) desde donde pueden subscribirse.

* hasta que los DNS se propaguen, se puede entrar por aquí.

Lenguajes Cuánticos de "Alto nivel"

Recientemente, Nacho publicó un comentario en mi blog en el que me mostraba un lenguaje de Computación Cuántica de alto nivel. Después, Mauro (desde su "nueva" ubicación), me pasó el dato de alguien de allí (Nottingham) que está trabajando con lenguajes de Alto Nivel para computación cuántica: Thorsten Altenkirch.

En su página pueden encontrarse varios artículos sobre sus trabajos. La verdad que me ha parecido un tema más que interesante, sobre todo por lo que planteé hace unos meses en el post Niveles de abstracción, pensando ingenuamente que aún no se estaba trabajando en ello. ¡¡Y hasta me encontré con un congreso sobre Lenguajes de Computación Cuánticos!!!

Debo decirlo: esto avanza muy rápido...

Cursos en el Instituto Henri Poincaré

Información, Computación y Complejidad Cuántica
4 de Enero al 7 de Abril de 2006

TOPICS

• Algoritmos cuánticos
• Comunicaciones
• Teleportación y criptografía
• Corrección de errores
• Información cuántica con variables contínuas
• Decoherencia y caos cuántico inducido por imperfecciones
• Implementación de qubits en estado sólido
• etc, etc...

Además, los siguientes eventos se llevarán a cabo:

• 16 al 20 de Enero: 9th International Workshop "Quantum Information Processing"
• 13 al 16 de Febrero: "QIPC Cluster Review and Conference 2006"
• 22 al 26 de Marzo: Workshop "Quantum computation and coherence"

Para más información dejo el Website del evento, y si algún alma caritativa me consigue una beca, nos veremos allá ;)

¿Quienes hacen la computadora cuántica?

La pregunta es: ¿Quienes están fabricando el Hard de la computadora cuántica?. Hasta ahora conozco las siguientes empresas:

• Hewlett-Packard (como lo comenté en un post anterior)
• MagicQ
• idQuantique
• D Wave
• ARTISTE COMPANY
  

¿Alguien conoce alguna otra?

Quantum Wiki

John Stockton ha creado el QWiki, un Wiki sobre Computación Cuántica. Y yo ya lo aprobeché creando mis artículos en Author y Paper ;)

Inversión millonaria por parte de HP y el Pentágono

Para la realización del prototipo de cómputo cuántico, la empresa HP anunció que la Agencia de Proyectos de Investigación Avanzada de defensa del Pentágono (Darpa), aportó diez millones de dólares al proyecto.

Los científicos e investigadores que trabajan en este proyecto, aseguraron que los equipos cuánticos compuestos por circuitos de rayos de luz, son más potentes que las computadoras electrónicas digitales fabricadas con transistores y además aceleraran el trabajo.

Estos equipos están basados en principios de mecánica cuántica, rama de la física que describe el mundo de las partículas subatómicas, aunque el potencial de la computación cuántica sigue siendo polémico.

Se han fabricado sistemas pequeños de demostración, pero hasta ahora los investigadores piensan que faltan más de diez años para poder hacer computadoras cuánticas a gran escala. Sin embargo, la compañía planea invertir más de siete millones de dólares en el proyecto, por lo que está diseñando un programa en su laboratorio para la fabricación de un prototipo.

(Por: Staff High Tech Editores)

Acercándonos a la máquina del tiempo

Una de las mayores dificultades para viajar en el tiempo ha sido resuelta por el físico teórico Amos Ori, del Israel Institute of Technology en Haifa (Technion)

Esta cita es de este artículo publicado en La Flecha en la que comentan sobre el reciente paper de Amos Ori[1].

Un científico israelí asegura haber resuelto una de las mayores dificultades para viajar en el tiempo, ya que su máquina no requiere materia exótica y utiliza el vacío que existe en el espacio para viajar a través del tiempo. Su máquina podría ser construida por una civilización más avanzada que la nuestra dentro de 100 o 200 años y elude las complicaciones de los modelos teóricos actuales, que requieren materia exótica (con una densidad de energía negativa y una presión negativa mayor en magnitud que la densidad de la energía) y una capacidad de ingeniería extraordinaria para recrear en laboratorio las energías de los agujeros de gusano. En cualquier caso, el viaje en el tiempo sigue estando en el ámbito de la especulación teórica, si bien hay nuevas propuestas para minimizar sus contradicciones filosóficas.

A quien le interese ver el paper original, éste se encuentra en la revista Physical Review Letters[1] (se necesita subscripción para poder bajar el texto completo por lo tanto lo dejo en mi página para el que lo quiera[2]) y el e-print está en la base de datos de los álamos[3] (descargable gratuitamente).

Referencias
[1] Amos Ori, "A Class of Time-Machine Solutions with a Compact Vacuum
Core", Phys. Rev. Lett. 95, 021101 (2005).
[2] AmosOri.pdf
[3] Amos Ori "A new time-machine model with compact vacuum core",
arXiv:gr-qc/0503077 (2005).

Circuito para distinguir estados de Bell desconocidos.

Recorriendo la Base de Datos de Los Alamos me he topado con un paper[1] más que interesante. Se trata de un circuito que logra distinguir entre los 4 estados de Bell, sin medirlos y sin destruirlos. El circuito planteado es el que muestro a continuación:

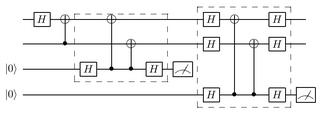
Es un circuito ingenioso que logra dejar en los dos qubits ancillares los valores de los qubits que generan el susodicho estado de Bell.
Me pareció un circuito muy "atractivo" hasta que noté que el mismo resultado puede conseguirse sin mucho esfuerzo "desentangleando" el estado de Bell y volviendo a entanglearlo, de esta manera:

por lo que el circuito anterior pierde todo sentido. En otro paper[2] hablan de cómo utilizar este algoritmo para clonar estados de Bell y el autor termina comparando su método con la Universal Cloning Machine[3] (UCM) diciendo que el suyo es extremadamente mejor ya que puede clonar con fidelidad 1, mientras que la UCM sólo lo hace con una fidelidad de 5/6. En realidad la cuestión es que la UCM clona cualquier estado desconocido, en comparación con éste algoritmo que copia sólo estados de Bell, los cuales pueden ser copiados por más de un método, ya que el Teorema de No-Clonning lo que dice es que no se pueden clonar estados no-ortogonales, y los estados de Bell son ortogonales entre si.

Referencias

[1] M. Gupta, P. K. Panigrahi, "Deterministic Bell State Discrimination", arXiv:quant-ph/0504183 (2005).
[2] J. O. Grabbe, "Deterministic cloning of an unknown Bell state", arXiv:quant-ph/0507016 (2005).
[3] D. Bruss, D. P. DiVincenzo, A. Ekert, C. A. Fuchs, C. Macchiavello, J. A. Smolin, "Optimal Universal and State-Dependent Quantum Cloning", Phys. Rev. A 57 2368 (e-print arXiv:quant-ph/9705038) (1998)

100 años de la Teoría de la Relatividad Especial

Hoy se cumplen 100 años desde que Albert Einstein publicó su artículo titulado "Sobre la Electrodinámica de los Cuerpos Móviles"[1] en cual define la Teoría de la Relatividad Especial. Feliz cumple, teoría ;)

Links interesantes:
* Explicación de la Relatividad Especial en la Wikipedia
* Traducción al inglés del paper original

Referencias:
[1] A. Einstein, "Zur Elektrodynamik bewegter Körper", Annalen der Physik. 17:891-921. (30 de Junio de 1905).

Algoritmo de Shor y Algoritmo de "de Vries"

En un nuevo paper de Andreas de Vries[1], parece ser que el algoritmo que plantea es capaz de realizar una búsqueda en una base de datos desordenada en un órden O(log n). Esto implica que NP está dentro de BQP, o sea: los problemas NP completos son resolubles en tiempo polinomial en una computadora cuántica.

Si esto es correcto, este nuevo algoritmo hace obsoleto el algoritmo de Grover y es, junto al algoritmo de Shor, uno de los más importantes algoritmos cuánticos.

Aún debo leerlo más "sesudamente", luego comentaré mis impresiones.

Update: Estaba leyendo el paper y encontré hasta ahora un error en la ecuación (9) donde dice que C²=C-I, esto no es cierto, pero igualmente, antes de terminar de leerlo encontré este post en el Weblog de Dave Bacon que ya lo estudió a fondo y encontró otros errores más. El paper fue enviado a la Physical Review D, así que será cuestión de tiempo de esperar a que lo refereen y de Vries corrija los errores, asimismo creo que la afirmación de que NP C BQP no se podrá demostrar a partir de este algoritmo.

Update++: En palabras del mismo Andreas, el problema más severo en su paper está en el Ejemplo 5, en el cual dice que su algoritmo es más rápido que el de Grover, y esto no es cierto, ya que para el caso especial de N=4 (el que él analiza) el algoritmo de Grover requiere una sóla consulta al oráculo, no 2 como dice él, y en ese caso su algoritmo se comporta exactamente igual, por lo tanto el algoritmo de Grover sigue siendo "óptimo".

[1] A. de Vries, Fast quantum search algorithms by qubit comparisons exploiting global phase interference, arXiv:quant-ph/0506137.

Niveles de abstracción

Veamos, el desarrollo lógico de la computación cuántica, al igual que la computación clásica, debería ir llevando a crear nuevos niveles de abstracción. Hasta ahora existen:
nivel 0 de abstracción: Física cuántica
nivel 1 de asbtracción: Computación cuántica en base a compuertas lógico-cuánticas
nivel 2 de abstracción: Aritmética computacional cuántica
nivel 3 de abstracción (¿o 1.5?): Lambda Cálculo para computación cuántica

Ya sería hora de crear un nuevo nivel, "lenguajes de programación cuánticos" ¿qué permitiría esto? si bien no se van a poder implementar "compiladores" cuánticos todavía (ya que no existen aún máquinas cuánticas que manejen un número de qubits interesantes), se puede llegar a simplificar bastante el escribir algoritmos cuánticos si disponemos de un lenguaje para esto. El único problema es que todos los "niveles" mencionados siguen desarrollándose constantemente, por lo tanto se necesitaría un lenguaje lo suficientemente potente como para poder ir cambiándolo facilmente de acuerdo a los nuevos descubrimientos en niveles inferiores.

Se invita a todos a dejar sus comentarios ;)

PD: si quieren saber un poco más de qué es la computación cuántica, lean el post anterior "Charlas Introductorias a la Computación Cuántica"

Charlas Introductorias a la Computación Cuántica

Terminaron las charlas, quería agradecer a Federico Bergero, Mariano Salvetti y Rafael Namías por la ayuda en la organización (y por haber sido los que propusieron el curso), a Guido Macchi, Claudio Gazza y Ariel Dobry por todo el apoyo y a Lucas Minuto por ser el conejito de indias escuchando cada charla antes de que la dicte.

Se puede bajar los apuntes completos de las charlas desde eXactas.org haciendo click acá.
Nuevo link (eXactas no existe más).

Mi primer Paper

Aún no está publicado, pero ya lo he enviado para su publicación, se puede ver el preprint desde la base de datos de Los Alamos[1].

En este paper, titulado "On the Teleportation of N-qubit States", lo que hago es una generalización del algoritmo cuántico de teleportación creado por Brassard[2] (basado en la teleportación descripta por Bennett et al.[3]) y además hago una generalización de los dos protocolos de teleportación que planteó Kak[4] (los cuales con tan sólo n bits de información clásica completan la teleportación, en contraste de los 2n bits necesitados en el protocolo de Bennett).
El único problema con los protocolos de Kak es que se necesita preparar el estado que se llevará "Bob" junto con el estado que se va a teleportar (por lo tanto no tiene mucho sentido, ya que en ese caso, sería más lógico que Bob se llevase directamente el estado que quiere obtener), igualmente a nivel teórico los protocolos de Kak, son interesantes.

Referencias
[1] A. Díaz-Caro, arXiv:quant-ph/0505009 (2005)
[2] G. Brassard, Physica D 120, 43 (1998)
[3] C. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres y W. Wootters, Phys. Rev. Lett. 70, 1895 (1993).
[4] S. Kak, arXiv:quant-ph/0305085 (2003)