El primero está basado en la tesis de licenciatura, en progreso, de Pablo Buiras. El paper lo escribimos entre Pablo, Mauro Jaskelioff, y yo (sus directores). Pueden bajar el paper libremente del arXiv: arXiv:1102.0749.
El título del paper es
Lower bounds for scalars in a typed algebraic λ-calculus
(Cotas inferiores para escalares en un λ-cálculo algebraico tipado)
The linear-algebraic λ-calculus is an untyped λ-calculus extended with arbitrary linear combinations of terms. As shown by previous works, building a type system on top of it is a delicate matter. A straightforward extension of a classic type system, like System F, would impose an undesirable restriction: it would only allow superpositions of terms of the same type. Adding sums of types lifts this restriction but raises the question of how to deal with the interaction between scalars and additions. We propose a type system with sums of types for the linear-algebraic λ-calculus which provides an answer to this question by allowing types to have some degree of imprecision. The proposed type system has a subject reduction property and is strongly normalising. Furthermore, we show that the additive fragment of the calculus can be seen as an abstract interpretation of the full calculus.
En lugar de traducir el abstract, explico un poquito la idea: En [DCP10] Barbara Petit y yo creamos un sistema de tipos, λadd, para el fragmento aditivo del linear-algebraic lambda-calculus [AD08] (λlin para abreviar). Luego mostramos que ese cálculo podía traducirse a System F con pares.
En el nuevo trabajo, extendemos ese resultado para el cálculo λlin completo: Primero creamos un sistema de tipos muy similar a λadd, pero para todo el cálculo: o sea, no sólo para lambda términos que se pueden sumar, como t+r, con t y r lambda términos, sino que también se pueden escalar: α.t+β.r, con α, β reales positivos. El sistema se llama λFA (por Full-Additive). La sintaxis de los tipos sigue siendo la misma que la de λadd : básicamente es Sistem F donde además se pueden sumar tipos. Y los escalares? Bueno, lo que hacemos es aproximarlos tomando su parte entera: si un término t tiene tipo T, el término α.t:⌊α⌋.T (nótese que ⌊α⌋ es un número natural y por tanto ⌊α⌋.T no es más que T+T+····+T, ⌊α⌋-veces). Como alguno ya inferirá, mezclar escalares y sumas no es nada sencillo, por ejemplo: 1/2.t+1/2.t tendría tipo ⌊1/2⌋.T+⌊1/2⌋.T = 0.T+0.T = 0, sin embargo si tomamos números mayores (por ejemplo, multipliquemos todo por 100), pues la precisión será muy buena... bueno, depende de lo que queramos decir por "muy buena", pero si no nos parece buena, pues agregamos más 0s al 100 :)
Probamos una especie de subject reduction para este sistema: básicamente lo que dice que se pierde precisión en los escalares al reducir el término, pero no en los tipos. O sea, si un término tiene tipo T+R+S+S, pues sabemos que al reducirlo (al "ejecutar el programa"), obtendremos un término con al menos los tipos T, R y dos veces S.
Además hicimos una prueba de strong normalisation: algo no sencillo ya que la prueba de Scalar [ADC09] no nos sirve porque en Scalar sólo se puede tipar t+r si t y r tienen el mismo tipo (módulo un escalar), por lo tanto el conjunto de términos no es el mismo. Tampoco se puede re-usar la de λadd, porque allí los escalares en los términos no existen (por lo tanto también tenemos otro conjunto de términos), así que hubo que hacer una prueba desde cero.
Por último, mostramos que λadd se comporta como una interpretación abstracta de λFA, y luego conjeturamos (con muchas pistas de que la conjetura es cierta), que System F con pares por extensión también es una interpretación abstracta de λFA.
-
El segundo paper es un trabajo con Pablo Arrighi y Benoît Valiron y es una extensión (o digamos, la continuación) de este. El título es:
A type system for the vectorial aspects of the linear-algebraic lambda-calculus
(Un sistema de tipos para los aspectos vectoriales del linear-algebraic lambda-calculus)
Abstract:
In this paper we describe a type system for the linear-algebraic lambda-calculus. The type system accounts for the part of the language emulating linear operators and vectors. The type system is able to statically describe the linear combinations of terms resulting from the reduction of programs. This gives rise to an original type theory where types, in the same way as terms, can be superposed into linear combinations. We show that the resulting typed lambda-calculus is strongly normalizing and features a weak subject-reduction.
Básicamente los cambios con respecto al viejo son: volvimos a agregar una regla de reescritura que habíamos quitado previamente (usando un truco para que ahora sí funcione), haciendo que el sistema sirva para todo el cálculo λlin, y lo más importante: λlin originalmente (el cálculo no tipado) podía encodear programas cuánticos. Ninguno de los sistemas de tipos en los que trabajé hasta ahora podía hacerlo, Scalar puede tipar programas con distribuciones baricéntricas, λadd podría pensarse como no determinista y λFA podrían ser usado para tipar programas probabilísticos, pero este es el primero que permite tipar los programas cuánticos propuestos en el paper original.
El cálculo se llama λvec (bueno, el nombre correcto sería 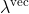 ).
).
Aún no lo subimos al arXiv, pero lo que vamos a hacer es actualizar el anterior, ya que es su versión final (ah, por cierto, el anterior, que sería la versión "work-in-progress" de este, fue aceptado y lo vamos a presentar en QAPL 2011 (sólo como presentación, sin aparecer en los proceedings ya que es un work-in-progress)).Cuando aparezca la versión nueva en arXiv pondré el link aquí. Lo pueden bajar de aquí: arXiv:1012.4032.
Aún no lo subimos al arXiv, pero lo que vamos a hacer es actualizar el anterior, ya que es su versión final (ah, por cierto, el anterior, que sería la versión "work-in-progress" de este, fue aceptado y lo vamos a presentar en QAPL 2011 (sólo como presentación, sin aparecer en los proceedings ya que es un work-in-progress)).

Alejandro, yo no se nada de esto, por lo que mi pregunta puede ser tonta. Pero en general, como se define un programa (o algoritmo?) cuantico en calculo lambda? Segun mi entendimiento, el calculo lambda es un lenguaje "descriptivo", i.e. solo indica que pasa en la computacion, y no como se hace. Entonces, las cuestiones de complejidad estan escondidas ahi. Pero, es en la complejidad en donde radica la gran diferencia en los algoritmos cuanticos y clasicos. Si solo se puede describir "lo que el algoritmo hace", en donde queda la complejidad?
ResponderBorrarHola Marcos.
ResponderBorrarEl cálculo lambda describe el "cómo". Por lo tanto bien podrías hacer un análisis de complejidad allí si quisieras. De todas maneras, no creo que sea lo más interesante hacer un análisis de complejidad en un algoritmo cuántico escrito en lambda-cálculo (puede ser muy complejo, y hay otras herramientas mejores para ello).
El cómo se define un algoritmo cuántico: bueno básicamente se toman las definiciones clásicas de true y false en lambda cálculo, se consideran que esos representan los ket |0> y |1>, y se escriben las compuertas cuánticas por descripción: por ejemplo, para la compuerta Hadamard que toma |0> y devuelve |-> y toma |1> y devuelve |+>, se escribe un término lambda que procurando que se comporte de esa manera con true y false, y el cálculo en sí (λlin) es "lineal" con respecto a la suma y los escalares, por tanto, si tenemos definido nuestra compuerta H que actúa como se espera en true y false, cuando hagamos H (α.true+β.false) vamos a obtener α.H true+β.H false (como se esperaría), debido a esa linealidad.
Hay muchísimos más detalles que estoy pasando por arriba. Te recomiendo el paper [AD08] que cito en el post si te interesa mirar un poco más profundamente el tema.
Con respecto a "para qué queremos ésto" (ya que como dije más arriba, no es para analizar complejidad), te recomiendo el post con el cual nos conocimos :) http://computacioncuantica.blogspot.com/2009/09/computacion-cuantica-teoria-de-tipos-y.html
Ahí explico la conexión entre teoría de tipos y lógica cuántica. El lambda cálculo tipado me interesará cuando logre que sólo los algoritmos cuánticos y nada más que los algoritmos cuánticos puedan ser tipados allí, y por tanto, su sistema de tipos se corresponderá con una lógica cuántica, desde un punto de vista computacional (o sea, más formalmente fundada que la lógica cuántica de Birkhoff y von Neumann).