Quisiera comentar un poco sobre lo que cuesta estudiar computación cuántica y computación teórica. Entiéndase "cuesta" en términos de esfuerzo, y no en términos de dinero.
Antes de empezar a estudiar el tema, había estado realizando investigación en búsqueda local para problemas de optimización combinatoria como SAT, TSP, etc. Aquí tienen un lista de mis
publicaciones. Estos temas los hacía principalmente con experimentos, y fui descubriendo de a poco que no quería hacer investigación experimental. Empece a estudiar computación cuántica con énfasis en algoritmos y complejidad computacional hace 2 años atrás. Ese fue mi plan para la escuela de post-grado. Actualmente ya me siento cómodo trabajando en esta área, tanto que ya estoy en condiciones de publicar resultados. Ahora mismo conferencias, y luego revistas.
La parte más complicada es construir una intuición. Para trabajar en computación teórica utilizamos generalmente las máquina de Turing como modelo. Acostumbrarse a ello no es fácil, y requiere mucho estudio para que se vuelva algo más natural. La mecánica cuántica es en mi opinión más difícil, porque las personas traemos instintivamente conceptos como velocidad, distancia, aceleración, etc., pero en el mundo cuántico no tenemos forma de percibir lo que ocurre. La intuición y el sentido común no sirven y tenemos que seguir los modelos que están bien probados experimentalmente. Es esa intuición la que requiere horas de estudio todos los días durante varios meses. Y no solamente leer sino también hacer investigación, e intentar resolver problemas. A continuación presento un lista de las cosas que considero necesarias para estudiar complejidad computacional y algoritmos cuánticos.
1- Algebra Lineal. Espacios vectoriales y sus propiedades, con principal énfasis en espacios de complejos.
2- Combinatorica. Contar objetos discretos por medio de permutaciones, combinaciones, etc, y otros conceptos muy importantes como series finitas e infinitas (aunque esto es más cálculo), funciones generadoras, aproximación de Stirling. Aquí también incluiría teoría de grafos combinatorica.
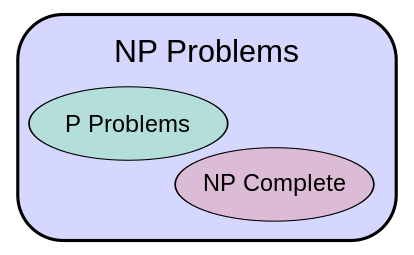
3- Complejidad Computacional. Las clases de complejidad básicas como BPP, P, NP, PSPACE, IP, SZK, P/poly, PH, y otros conceptos como relativización y reducciones. También agregaría otros modelos de computación como "communication complexity", árboles de decisión, PCP, y "derandomization".
4- Fundamentos de Computabilidad / Teoría Recursiva. Las definiciones de autómatas como modelos de computación, problemas decidibles, no-decidibles y semi-decidibles, la jerarquía aritmética, y más reducciones. También modelos descriptivos como cálculo-λ y funciones recursivas.
5- Probabilidades. Los conceptos básicos de espacio de probabilidades, valor esperado, varianza, distribuciones de probabilidades, momentos de una variable aleatoria y como realizar análisis probabilístico de algoritmos y análisis de algoritmos probabilísticos. Es de vital importancia también aquí la teoría de cadenas de markov y el método probabilístico en sus distintas formas.
6- Análisis Funcional. Los conceptos de espacios de Hilbert, espacios con normas, y espacios métricos.
7- Análisis Complejo. Analiticidad, ecuaciones de Cauchy-Riemann, funciones armónicas, algebra de números complejos, integrales de contorno. De aquí tuve que aprender un método para aproximaciones asíntoticas de integrales conocida como el método del punto silla.
8- Algebra Abstracta. Teoría de grupos, anillos y campos de Galois. Aquí pondría teoría de grafos algebraica e incluir "expanders" y grafos de Cayley.
9- Mecánica Cuántica. Postulados de la mecánica cuántica, el operador de densidad, estados cuánticos mezclados y puros, osciladores armonicos, dualidad partícula vs onda, el Hamiltoniano, etc.
10-Teoría de la Información. Cantidad de información y entropía, códigos, compresión.
No creo que sea una lista exhaustiva, pero es eso más o menos lo que tuve que estudiar y aprendí en las clases y fuera de ellas. Algunas ya las había aprendido durante los estudios de pre-grado, y otras en post-grado. Por ejemplo, el método probabilístico utilizando segundos momentos y el "Lovász Local Lemma" lo aprendí por mi cuenta, mientras la clase de complejidad SZK lo aprendí en un clase de post-grado sobre criptografía.
Por supuesto, es imposible acordarse de los detalles de todo, por lo que siempre hay que estar con los libros cerca. Pero por lo menos habría que recordar siempre los resultados principales.
Me imagino que en el área de lógica (donde trabaja Alejandro) debería de haber más cosas. No me imagino cuáles. Las comunidades de complejidad y computabilidad están un poco separadas. Comenzaron unidas pero luego fueron separandose debido a que las técnicas utilizadas eran muy diferentes unas de otras.
Aún habrán más cosas por aprender sin duda.